
This is a companion web page for several of my papers on spherical perspective, in particular my main paper on the subject: Ruler, Compass, and Nail: Constructing a Total Spherical Perspective, published by Taylor and Francis in the Journal of Mathematics and the Arts.
If you don't have access to the journal, you can download my latest author's manuscript here:
Ruler, Compass and Nail: Constructing a Total Spherical Perspective (version of 11jan2019).
This author's manuscript contains a small number of corrections and improvements over the published version.
You can cite the published version as:
António Bandeira Araújo (2018) Ruler, compass, and nail: constructing a total spherical perspective, Journal of Mathematics and the Arts, 12:2-3, 144-169, https://doi.org/10.1080/17513472.2018.1469378
I believe that articles should not, in our age, be static objects. So I will keep evolving this article as I feel is required, but please cite the published version whenever possible (unless a certain correction is essential for your purposes) because unfortunately I still haven't got a good versioning system in place that works well with citations. Hopefuly this will change in the future. Also, of course, versions subsequent to publication have not been peer reviewd.
In the 1960s, Barre and Flocon wrote a seminal book ( La perspective curviligne, 1967, Flammarion, Paris) wherein they defined a spherical perspective in a way that allowed for systematic drawing by elementary means, that is, by ruler and compass. However, "spherical perspective" was a bit of a misnomer since those rules were only specified for half the sphere. In this paper I extend those systematic constructions to the whole sphere. This extension had been attempted before, but either not successefuly or not systematically/completely. With this paper I solve the total spherical perspective in the same sense that Barre and Flocon solved the hemisphere: that is, I give a systematic method to calculate and draw all lines and vanishing points with ruler and compass (or even freehand). I also summarize Barre and Flocon's method in a very simple way (reduced to about two pages). Furthermore, I take the opportunity to consider what is the nature of a perspective as a mathematical object. I think it should be seen as a game of compactification that has anamorphosis as its central player (see the paper for details).
The initial title of the paper was "A construction of a spherical perspective in ruler, compass, and nail". It alludes to the fact that a set of (abstracted) mechanical apparatus defines a scope - it permits a certain class of points to be obtained from another through its action. Although you can construct the total spherical perspective with ruler and compass operations, I found that a more natural way to think about it is to imagine that you are using (or actually use) a third mechanical implement - namely, a nail fixed at the center of the page. This nail, interacting with a ruler, allows the construction of the antipodal image of a given meridian, and hence to construct the total spherical perspective by piggybacking on the hemsipherical constructions of Barre and Flocon.
Later, I have used the "nail" to implement a grid-based system that exploits the rotational symmetries of fisheye perspective, to make an easy system for outdoors drawing (urban sketching) of spherical perspective. I have taught this system at a Bridges workshop in 2019, and at many invited workshops all over the world, from Hong Kong to Brasil.The Bridges paper is here: A fisheys Gyrograph: Taking spherical perspective for a spin).
The method presented in this paper led me to other developments. I've been teaching courses on anamorphoses to all manner of students, ranging from primary school to Ph.D. students at our Digital Media Art Ph.D. (DMAD) at UAb. Later I find that my view on anamorphosis can be seen as a modern reframing of Euclid's Optics, which came as a surprise and that my view of of perspective can be seen as an Euclid-meets-Taylor kind of scenario. One is never original (more on that later, on a chapter coming out from Springer Nature, late 2020). This view of anamorphosis led me to naturally develop hand-drawing methods for other spherical perspectives. I published a solution for equirectangular perspective, which allowed me to mix perspectives with VR visualization. I have also developed a gridding system (see the Bridges paper ) for equirectangular perspective, using translational symmetries , and am currently developing a little piece of software (early alpha stage) to help me teach this perspective in workshop, called Eq A Sketch 360 (available here).
The paper was first published online as an arXiV preprint 2015, and it went through several versions, but the main results are unchanged from the first version, although there are many changes to citations, figures and section/theorem numbering, as well as to the text itself. The paper's title also changed twice. My favorite title was the second, the final one being in part an adaptation to editorial requirements.
The old arXiV preprints are at ArXiv.
Please let me know if you find any typos or errors in the article. At the moment the known corrections are as follows:
1 - On page 153, line 19 (the line above equation 1), where it reads
" the perspective map f " it should read " the perspective map p "
All of these need some work before I place them here, so I'll ask you to come around somewhat later (hopefully not infinitely long); I'll be working on it as my other duties allow.
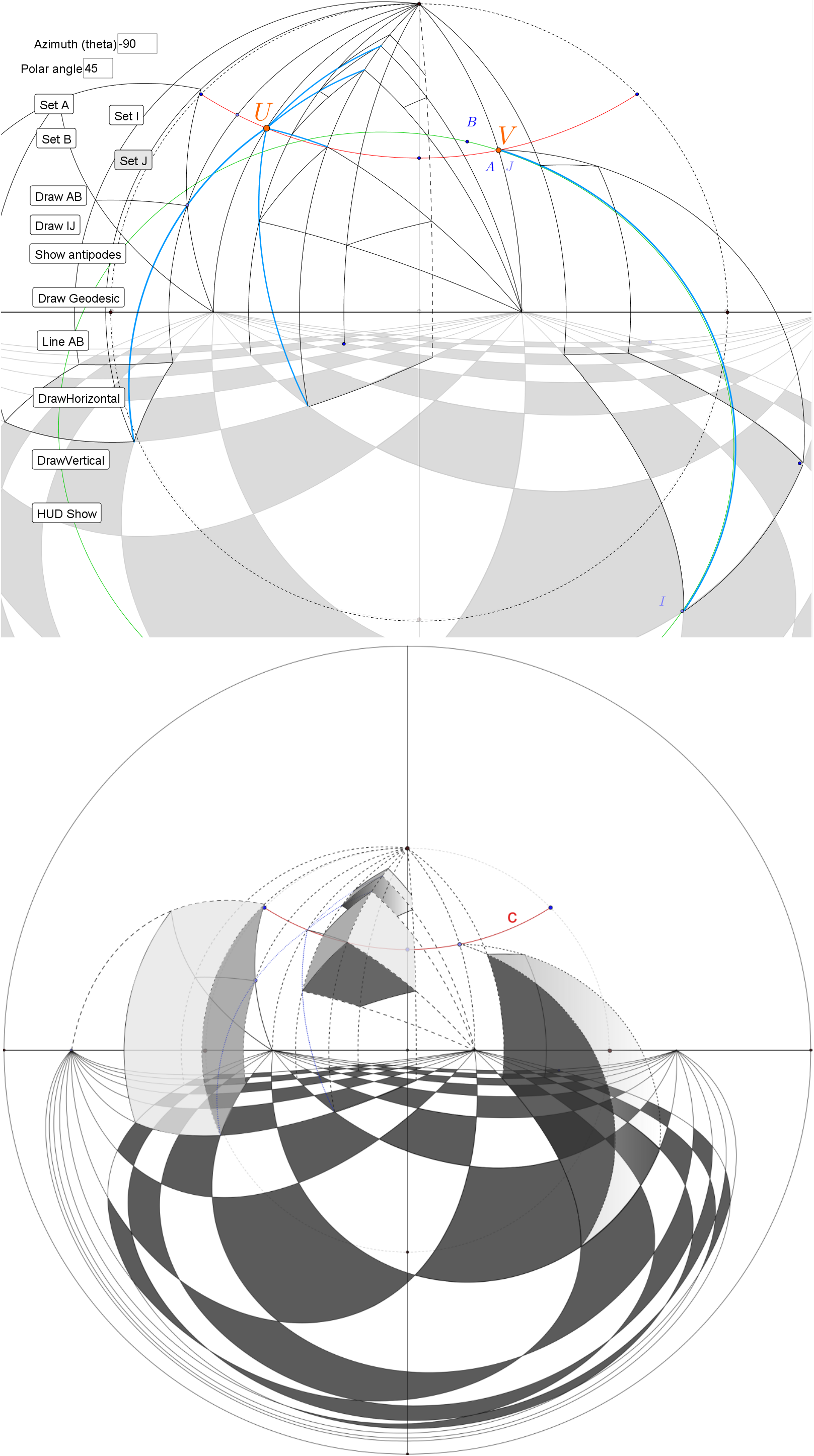
I made a simple GeoGebra tool for drawing the azimuthal equidistant (360-degree fisheye) spherical perspective. You can find it here:
I wrote a small paper about it. You can find it in the proceedings of the ARTeFACTo 2020 conference (pages 150-155).
It works by giving you 4 control points: A and B to define a geodesic (image of a plane) and I and J inside this geodesic to define the image of a line. This is all you need if you understand how to draw in spherical perspective.
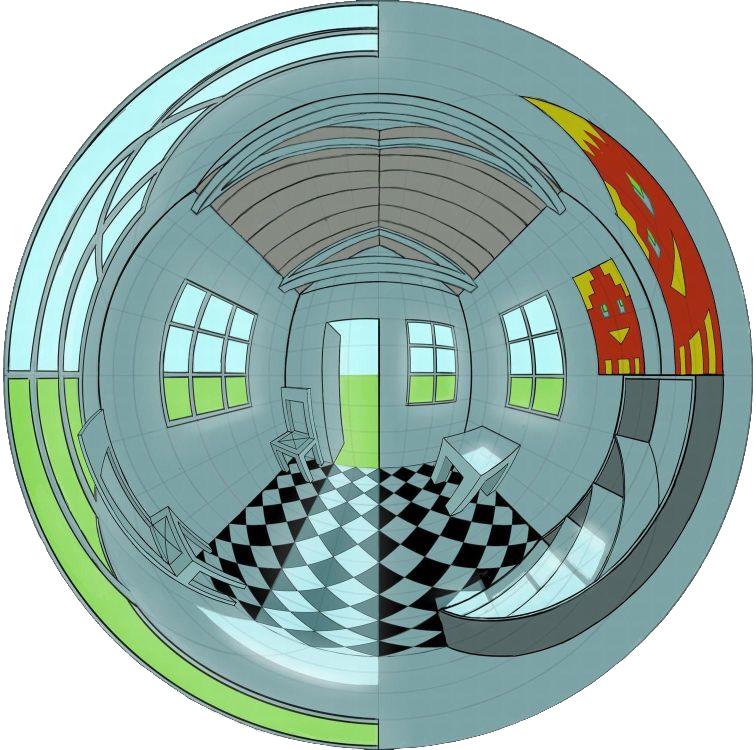
I made it for drawing nice vectorial illustrations for my papers, like the one below. It can be very useful when used as part of a pipeline: I did the perspetive work in the GeoGebra app and then moved it to inkscape for coloring.
Let me know if you find any use for it in your own work.
António Araújo, DceT, Universidade Aberta Antonio.Araujo@uab.pt Homepage