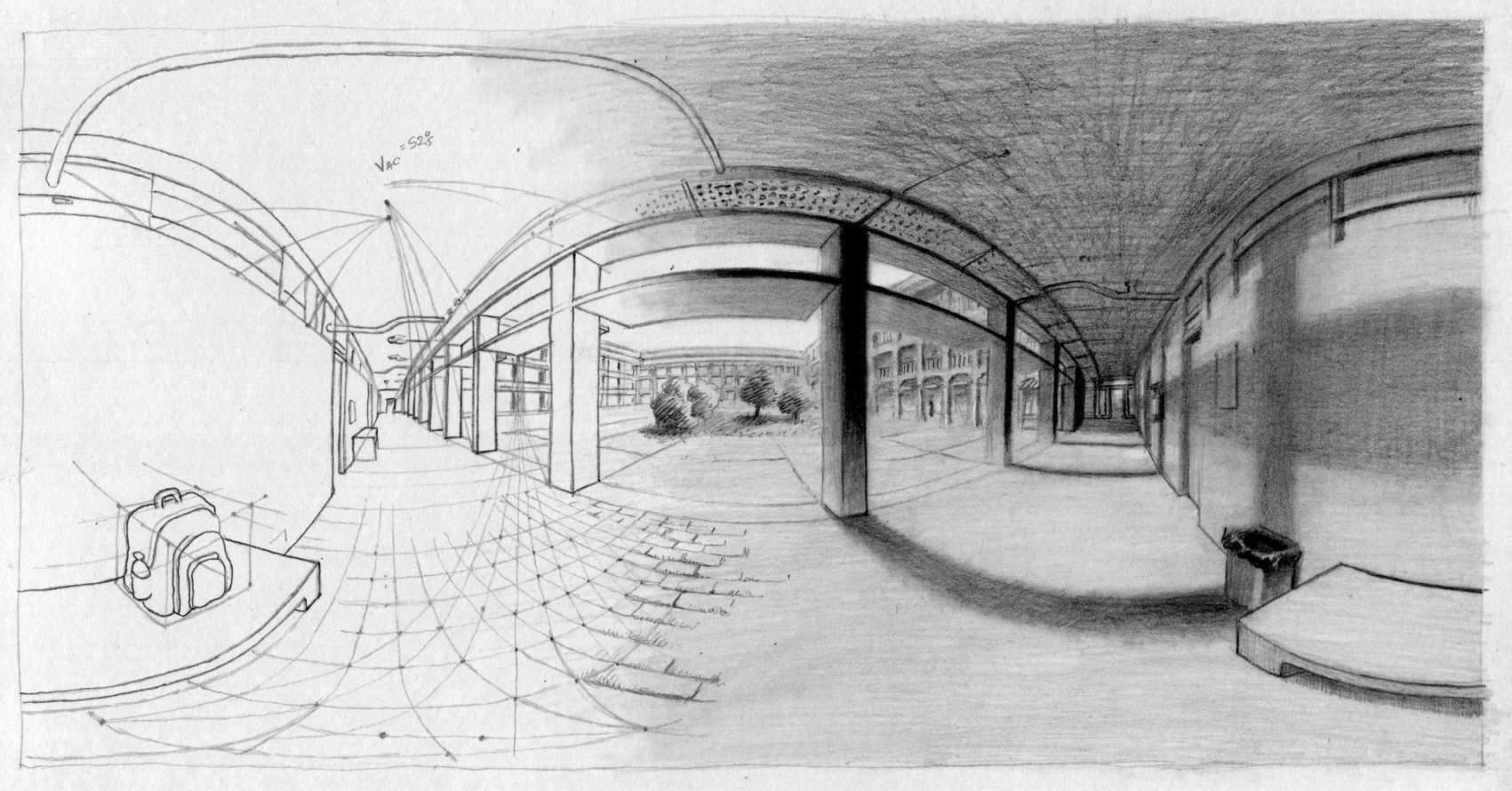

This is a hybrid artwork. On the one hand, it is a simple sketch of a real environment, done from observation, in the tradition of urban sketching. On the other hand, it is a generator for a virtual reality panorama. You can see a version of the panorama below. I did several versions of the sketch, with slightly different emphasis. The one above exhibits both the perspective construction and the finished rendering. The ones below separate the two aspects.
First let us see the fully rendered drawing and its VR visualization. Let us begin with the drawing. It is an equirectangular perspective drawing of ISEL's inner courtyard (ISEL is an engineeering school in Lisbon). I did a first sketch while I waited to give a lecture there. I measured carefully only a few spots, including the closest arch. Then I finished the rendering at home from my measurements.
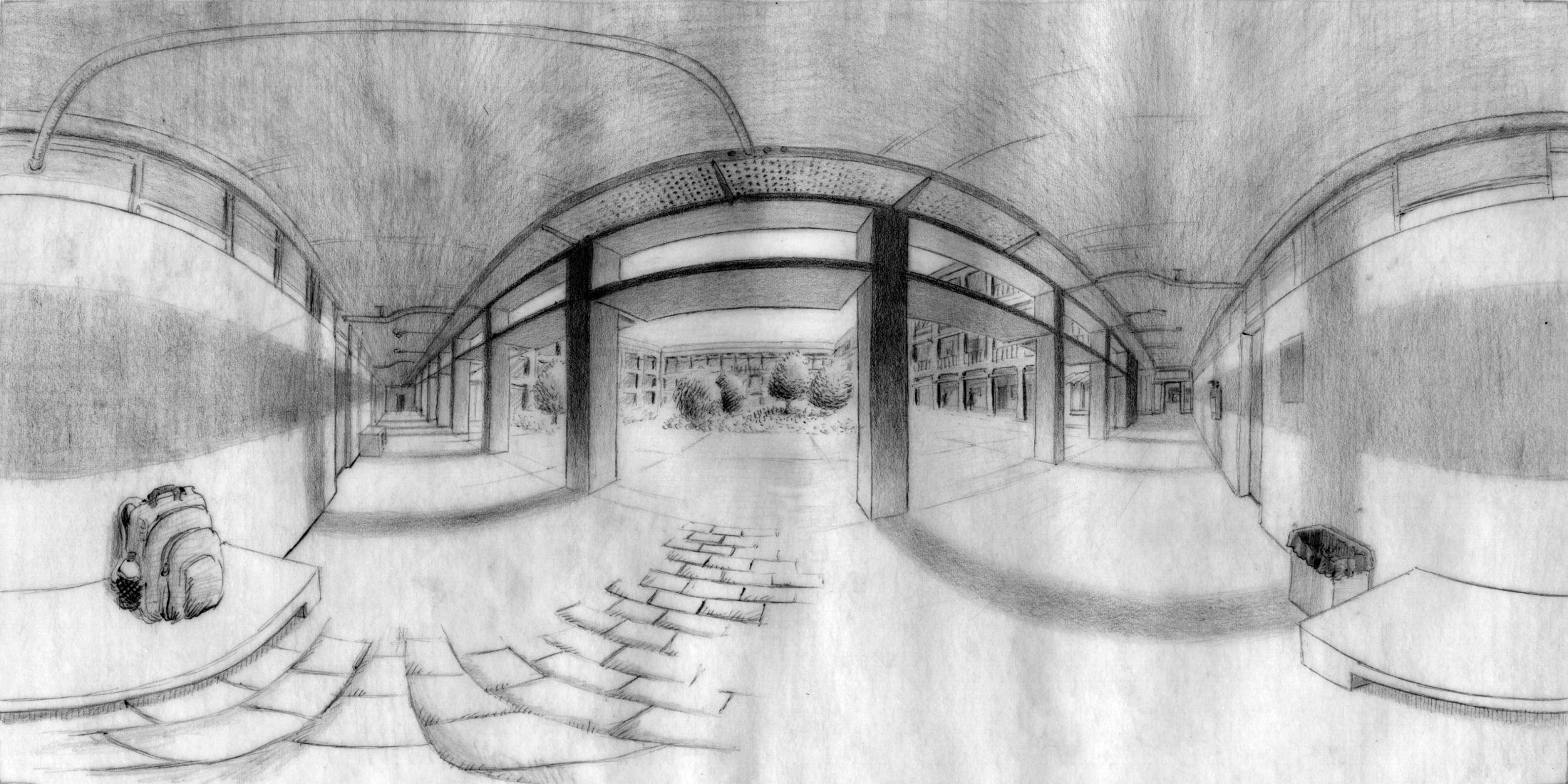
The good thing of drawing in equirectangular perspective is that the associated projection gets read as a 360-degree photo in flickr, facebook, etc. So if you did the drawing properly it can be seen immersively. Click and then drag below to look around the picture as if you were inside the original environment. This is a VR panorama.
Click on the picture below to see it as a VR panorama.
The drawing uses the rather objective, even journalistic rendering of a location as an excuse to demonstrate a perspective construction: perspective multiplication. I only measured the closest of the arches. The others I got from a process of perspective multiplication, by passing a diagonal across the arch, finding the vanishing point of that diagonal, and then sending iteratively parallels to that same vanishing point to find the next arches.
This is sometimes called the "telephone pole" problem in classical perspective. It has a more elegant solution here because this perspective (equirectangular spherical perspective) is complete and compact. Meaning, all lines have exactly two vanishing points, which are guaranteed to be in the rectangle of the picture.
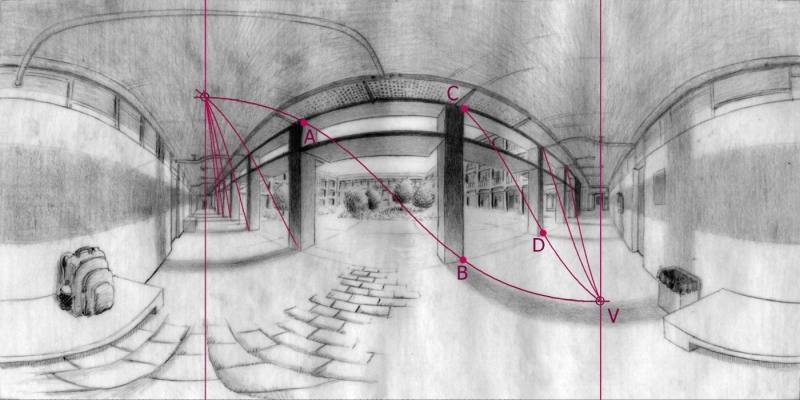
Below we can see the actual constructions I used in the preliminary drawing. You can see multiple uses of perspective multiplication, among other perspective techniques.
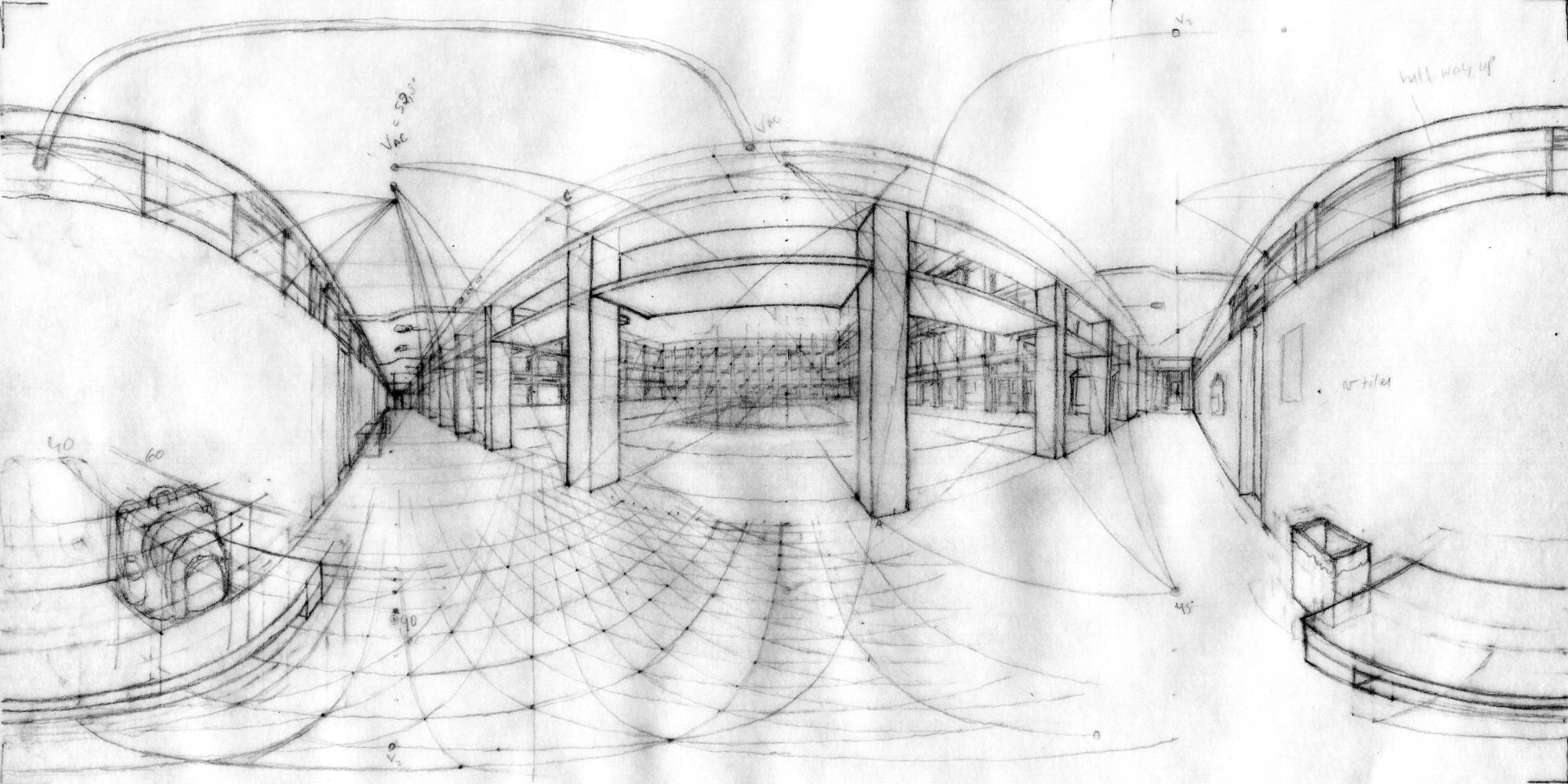
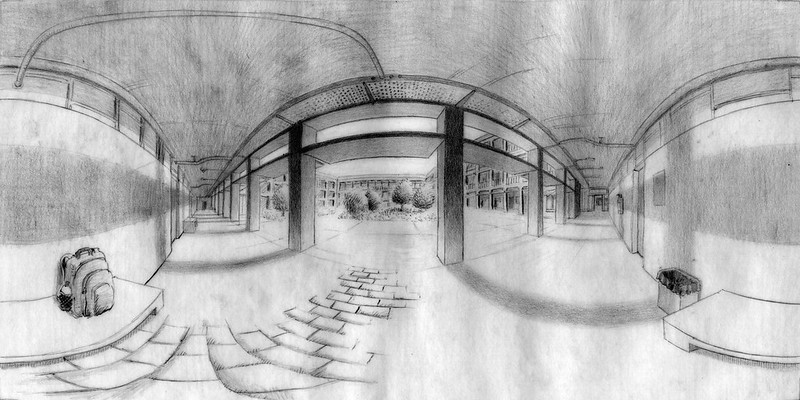
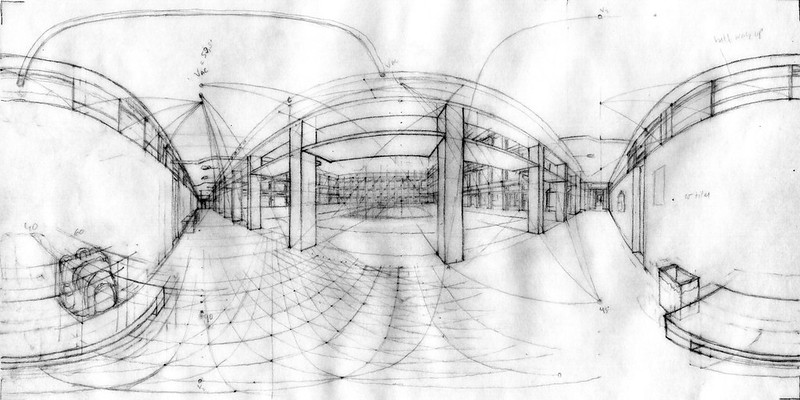
Below you can also see the VR panorama of this preliminary scaffolding. Notice how the curved lines of the spherical perspective become straight when seen in the VR panorama. In exchange, you lose the ability to see the two vanishing points of a line at once. This is the duality between spherical anamorphosis and spherical perspective.
Click on the picture below to see it as a VR panorama.
The ability to do these drawing is predicated on being able to draw equirectangular lines between two points. In the video below you can see how I did it in a simple way that lends itself to outdoor sketching.
I am using what I call the sliding grid method, which I introduced in my paper, Drawing Equirectangular VR Panoramas with Ruler, Compass, and Protractor.
Further readings:
You can learn more about my work by following links to my other pages and papers. You can learn more about handmade drawings of equirectangular perspectives, or you can try out my little app, Eq A Sketch 360, for drawing them digitally. Or perhaps you prefer to learn about fisheye spherical perspective. Or you can see my institutional page for a list of my papers.